Es conocida la frase (como chiste) que dice que hay tres tipos de engaños: las mentiras, las grandes mentiras, y las estadísticas.
La Estadística, como tal (así con mayúscula al principio), es una rama de la matemática, y como tal uno supondría que es exacta y precisa, y que no da para ambigüedades.
No sólo no es tan así, sino que muchas veces los resultados de usar estadística es una colección de números que hay que saber interpretar.
Este post es sobre un caso conocido como la Paradoja de Simpson (porque Edward H. Simpson la describió en 1951, aunque ya la habían mostrado Karl Pearson en 1899 y Udny Yule en 1903), que muestra un caso sencillo y particular sobre la (mala) interpretación de resultados estadísticos.
La idea acá es que más allá que se enteren de este caso en sí, empecemos a acostumbrarnos y tomar como normal criticar los números que nos muestran como "resultados" en cualquier noticia o publicación, que empecemos a tratar de entender de dónde vienen esos números, cómo fueron calculados, y de ahí validar (o no) las conclusiones que nos muestran.
Entonces, se las cuento.

En los ochenta se hizo un estudio sobre tratamientos para curar piedras en los riñones. Fue un estudio real, con la idea de comparar qué exito tenían en la curación de dicho problema dos tratamientos médicos distintos (involucrando procedimientos quirúrgicos abiertos y cerrados).
Para el estudio se consiguieron 700 personas con este inconveniente, y a la mitad se le hizo un tratamiento (llamaremos A) y a la otra mitad otro (el B). De esos 700, 357 tenían piedras pequeñas en los riñones, y 343 tenían piedras grandes.
La siguiente tabla muestra los cuatro grupos que quedaron (con Gn nombramos cada uno), incluyendo la cantidad de personas a las que se le hizo el tratamiento y la cantidad que se curaron. Por ejemplo el Grupo 1 fue de 87 personas, que tenían piedras chicas y se les realizó el tratamiento A; de ese total se curaron 81 individuos.
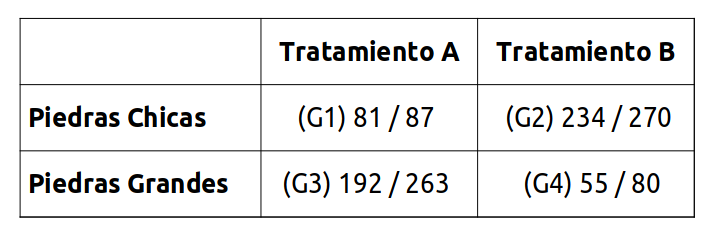
Hasta acá tenemos la información pura y dura. No está sometida a ninguna interpretación.
Pasemos ahora a leer los números :)

Analizando la información
Miremos qué pasó con los pacientes con piedras chicas. Los que recibieron el tratamiento A (grupo 1) se curaron en un 93% (81/87), mientras que los del tratamiento B (grupo 2) se curaron en un 86% (234/270). ¡Es mejor el tratamiento A!
Ahora, los pacientes con piedras grandes. Los que recibieron el tratamiento A (grupo 3) se curaron en un 73% (192/263), mientras que los del tratamiento B (grupo 4) se curaron en un 69% (55/80). ¡Es mejor el tratamiento A!
Conclusión, es mejor el tratamiento A. ¿Cierto?
Bueno. Supongamos que en vez de mirar de forma discriminada por tipo de piedra en los riñones, miramos en su conjunto qué pasó con los distintos tratamientos. Para ambos tratamientos tuvimos 350 pacientes en total. Con el tratamiento A se curaron 273 pacientes (81+192, un 78%), mientras que con el tratamiento B se curaron 289 (234+55, un 83%).
¡Es mejor el tratamiento B! ¿Ciert... pero qué carajo?
¿Es mejor un tratamiento u otro sólo con saber qué tipo de piedras tiene en los riñones? ¿Es mejor no medir el tamaño de las piedras y hacer el tratamiento B, o si ya sabemos el tamaño de las piedras de un paciente, hacer el tratamiento A (más allá de cual sea ese tamaño)?
No puede ser.
La paradoja
En el estudio hay una variable escondida, que es el tamaño de las piedras. Si consideramos esa variable, vemos que influencia fuertemente los tamaños de los grupos. Los grupos 2 y 3 dominan el estudio, mientras que los 1 y 4 son pequeños en comparación.
Esta variable escondida también tiene un efecto en los porcentajes de éxito, incluso es más influyente esta variable escondida que la elección del tratamiento.
En realidad el tratamiento A es mejor que el B, pero al considerar los totales parece lo contrario porque justo tuvimos un montón de piedras grandes (que son más difíciles de curar) con el tratamiento A, mientras que el tratamiento B justo se aplicó en su mayoría con las piedras pequeñas (más fáciles de curar).
En otras palabras, el factor "tamaño de las piedras" supera totalmente al factor "tipo de tratamiento". Sí, el tratamiento A es mejor que el B, pero en realidad la mayor probabilidad de curarse es teniendo piedras pequeñas y no grandes.

