Uno de los típicos problemas con los que uno se encuentra cuando hace algún programa es el de estimar cuanto falta para terminar una tarea (E.T.A. por sus siglas en inglés).
Analicemos esa oración con detalle.
Sí es típico, es que sucede muchas veces, no sólo a un programador, sino a muchos. Pero que uno se presente con el problema, y se siga presentando siempre con el problema, significa que todavía no está resuelto. O al menos no de forma genérica y satisfactoria.
Que queramos estimar, y no calcular exactamente cuánto, implica que es suficiente con dar una idea de cuanto falta. Consideremos que esta indicación es para el usuario impaciente que está mirando la barrita de progreso, o que abre cada tanto la aplicación y estima si la película que está bajando va a terminar para después de la cena o mejor busca algo en la tele. No hace falta decirle que calculamos terminar a las 19:33, pero es importante saber si esperamos que finalice a las 19, a las 20, o mañana...

Entonces... ¿por qué no está resuelto todavía de forma genérica y satisfactoria? Porque no es tan simple como parece. Veamos por qué. Por un lado, la velocidad con la cual estamos completando la tarea puede variar, y por el otro, le tenemos que dar una indicación a un humano. Y ambos son dos quilombos totalmente distintos... y complicados.
La velocidad con la cual vamos completando la tarea es todo un tema, porque si estamos descargando un archivo, podemos tener el problema de que la conexión se corte, por ejemplo, o que pongamos a bajar algo y la velocidad caiga a la mitad. Venía pareja, de repente baja a la mitad, y luego queda en ese nivel por el resto de la descarga. Como un escalón. O podemos estar reordenando una estructura, y sabemos cuantas partes nos falta reordenar, pero no tenemos ni idea cuanto va a tardar reordenar cada una de esas partes.
Y como decía antes, la indicación es para un humano. Si le muestro siempre el mismo número, no le sirve. Si le cambio el valor de 1 a 34 y después a 2 y a 38, y a 0, y a 50, cambiando cinco veces por segundo, tampoco le sirve. Y agreguémosle componentes sicológicos, como no mostrarle que la velocidad cae si sólo cayó por un momento porque es feo que vaya más lento (aunque sea verdad).
De algunos de estos inconvenientes estuvimos hablando la vez pasada en una conversación de PyAr. A mi me quedó colgado el tema en alguna esquinita del cerebro, y estoy finalmente escribiendo esto.
Requisitos
En general, podríamos definir las necesidades de nuestro algoritmo como las siguientes:
Tiene que ser fácilmente legible por el humano. Debería cambiar, máximo, dos veces por segundo si uno tiene buena vista. Si hay que prestarle atención al nro, una vez por segundo está bien.
Debe estimar lo mejor posible el tiempo faltante para terminar, pero nos tomamos la libertad de mentirle al usuario algunas veces si es para mejorar la calidad del indicador.
No tiene que depender de la aplicación: deberíamos encontrar un algoritmo que se desempeñe como corresponde más allá de qué estemos midiendo.
En función de eso, vamos con algunas consideraciones que he estado elaborando, leyendo en la lista de correo, en otros lados, o que ya tenía en mi cabeza desde antes. Pero para que nos entendamos mejor, vale una aclaración.

Todo el trabajo, donde la magia reside, es en calcular la velocidad estimada con la cual vamos a estar desde ahora hasta el final de la tarea. De esa manera, en función de lo que falta para terminar (en KB descargados, partes del archivo a procesar, o lo que sea), podemos estimar cuanto falta en tiempo, y consecuentemente le podremos mostrar al usuario cuando terminaremos.
Esa velocidad estimada con la cual vamos a estar desde ahora hasta el final de la tarea la llamaremos, como corresponde, de alguna manera más corta. Como esa velocidad es calculada en función de la experiencia obtenida en lo que va de la tarea, normalmente se llama Velocidad Promedio, pero no crean cuando lean ese nombre que es, justamente, la velocidad promedio, sino que es la velocidad calculada con el algoritmo que estamos tratando de encontrar, con un nombre corto, :).
Simulando
Antes de comenzar a discutir cómo calcular nuestra ya famosa Velocidad Promedio, tenemos que encontrar alguna forma de simular el estímulo.
Es decir, deberíamos hacer un programita que nos vaya dando valores simulados para probar las formas de cálculo de la Velocidad Promedio (de otra manera, tendríamos que incorporar esas distintas maneras a sistemas reales, lo que dificultaría muchísimo probar y ver qué nos gusta más y qué nos gusta menos).
Entonces me armé un generador de valores, que será la fuente de nuestros ejemplos. Las reglas del generador son sencillas, porque no quería perder más tiempo armando el simulador que jugando con lo otro. Así y todo, aunque a veces tira escenarios raros, la mayoría de las veces funciona como esperamos.
Comienza generando en cero, y permanece tres valores en cero, como si fuera tiempo de conexión, una especie de inactividad inicial. Luego pega un salto de 50, o sea que se conectó de golpe y comienza a tener "vida". De aquí en más, siempre con limitado al rango de 0 a 99 (inclusives), los valores van variando al azar, con el siguiente comportamiento:
El 1% de las veces se desconecta, tira 10 valores en cero y luego trata de volver (lo logra el 10% de las veces, y vuelve al valor que tenía antes)
El 4% de las veces genera picos de 2 valores de ancho, de +/- 40 (luego de los dos vuelve al valor que tenía antes)
El 70% de las veces varía al azar sumando alguno de [-2,-1,0,1,2] (obvio, si suma -2, es que baja dos puntos)
El 15% de las veces varía al azar sumando alguno de [-5, -4, ..., 4, 5]
El 10% de las veces varía al azar sumando alguno de [-10, ..., 10]
¿Entonces? ¿Cuánto falta?
Un concepto que usé desde entrada (concepto bastante básico) es el de tomar no todos los valores para calcular la Velocidad Promedio, sino sólo algunos últimos (analogía eléctrica: es como si estuviésemos pasando la señal por un filtro pasabajos). Esto tiene el efecto de calmar el indicador que mostramos, siendo no tan nervioso sino que variará más tranquilamente.
El truco es cuantos valores tomar para este promedio. Y como no podemos ver el futuro y saber de entrada la mejor cantidad para este cálculo, la mejor manera que se me ocurrió es tratar de ir adaptándose.
El primer modelo que armé agranda o achica la cantidad de valores a tomar en función de cuan nervioso esté el indicador. Si se pone nervioso (es decir, varía mucho de valor a valor), agrandamos en uno la cantidad de valores. Y si se tranquiliza, achicamos en uno la cantidad.
El segundo modelo también agranda o achica la cantidad de valores. Pero ahora, cuando está nervioso, en lugar de incrementar en uno y seguir, vamos incrementando hasta que lo notamos lo suficientemente tranquilo. Y si luego se estabiliza, achicamos (como antes), la cantidad de puntos en uno.
El tercer modelo trata de tranquilizar el indicador de otro modo. Tomamos siempre la misma cantidad de valores, pero nos fijamos en cual fué la variación mayor en ese grupo, y cual es la variación entre el último y el nuevo valor. Si esta última variación es mayor a la que veníamos teniendo, tomamos eso como símbolo de nerviosismo y no usamos el último valor para el promedio, sino uno recortado.
El siguiente es un ejemplo de los tres modelos para el mismo conjunto de valores simulados (primero a tercer de arriba para abajo). Tienen más ejemplos aquí y aquí, y el código que genera todo aquí.
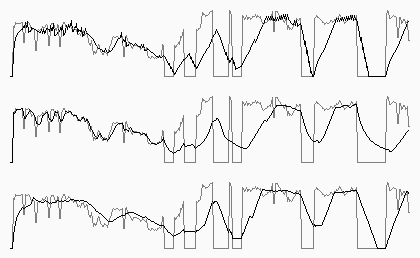
Como ven, el tercero es el que más tranquilo parece, y así y todo luce responsivo a los cambios de largo o mediano plazo. A mí es el que más me gusta. Pero tiene una falla segura: la cantidad de puntos a tomar en el promedio permanece constante (en este caso, está prefijada a 20).
Cambio de punto de vista
Me puse a pensar entonces en como podía tener este tercer modelo más adaptativo (o sea, que la cantidad de valores en el promedio no esté fija en 20 sino que vaya subiendo y bajando en función de algo más).
Y me di cuenta de que las reglas que determiné arriba quizás estén incompletas, que se les podría agregar la siguiente:
Debe tener en cuenta, en lo posible, en qué parte del proceso de completamiento estamos.
O sea, que el sistema quizás se comporte distinto, estimando diferente, si estamos en la primer parte de, digamos, la descarga, en la mitad, o cerca del final. Por ejemplo, si estamos a un 40% de la descarga, está bien que tomemos valores tranquilos, porque falta un montón y tenemos que estimar lo que viene. Pero si nos falta un 5%, ¿tiene sentido que tomemos el otro 95% como indicador? Porque cualquier variación, faltando tan poco, tiene una alta incidencia en el tiempo que nos falta para terminar.
Entonces desarrollé otro simulador, pero ahora con una lógica distinta, ya que en este calculamos lo que nos falta para terminar. Fíjense en las siguientes dos curvas, que tenemos en gris las velocidades reales, en negro la Velocidad Promedio, y en azul lo que le diríamos al usuario que falta.
En la curva de arriba pueden ver el comportamiento del modelo C de la etapa anterior, y en la inferior, el mismo modelo, solo que ajustamos la cantidad de valores para realizar el cálculo en función de por donde estamos de la descargar (lo que hacemos es tomar todos los valores hasta que llegamos a la mitad, y luego de la mitad la cantidad de lo que faltaría para terminar). Más allá de si nos gusta más o menos, este nuevo modelo tiene la complejidad de saber cuantas unidades falta para terminar (podemos saberlo si estamos descargando un archivo del que conocemos el largo total, pero no de otra manera, por ejemplo).
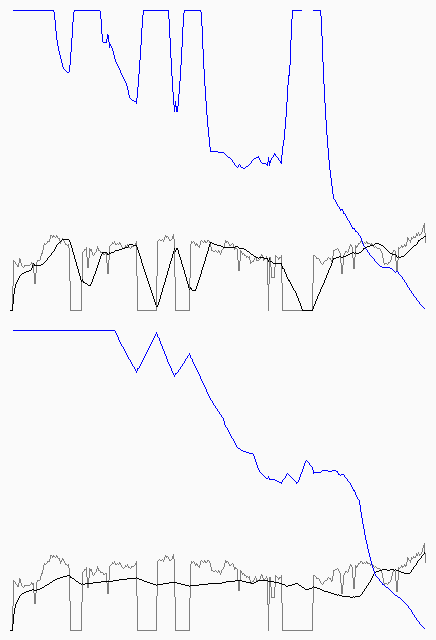
Fíjense que en este nuevo modelo no estamos generando la misma cantidad de puntos siempre para la simulación, sino que arrancamos con una determinada cantidad para descargar, y seguimos hasta que se descargue todo (por eso el ancho de los ejemplos es variable). Noten también que recorté en un máximo la indicación del usuario, para que el detalle inferior se vea mejor.
Tienen dos ejemplos más acá y acá, pueden generar más con este programa.
Conclusiones
Luego de cotejar ideas, gráficos, probar mil y una veces, no llegué a encontrar el modelo que yo diga "¡Este!". Pero el que creo que más se acerca a como a mi me gustaría que se comporte, es este último (lo cual no es mucha casualidad, ya que es el último porque lo fui trabajando, esto fue una evolución).
Así y todo, no tengo manera de demostrar que este es el mejor, y eso se debe en gran parte porque las pautas iniciales eran claras, pero vagas. Quizás si alguien apareciese con una mejor explicación de cómo se debería comportar el sistema, fuese más fácil lograrlo.
Pero creo que el 90% de la complejidad de esto es, justamente, que no tenemos muy en claro cómo se debe comportar.
Así y todo, creo que este análisis sirve, aunque sea porque para demostrar que estoy equivocado vas a lograr un mejor resultado, :D
Ah! Y un resultado secundario, es que me divertí mucho tirando curvas con PIL, la biblioteca para imágenes en Python.

